Triangles ⇒⇒ Exercise 6.2

Question 1 (i)

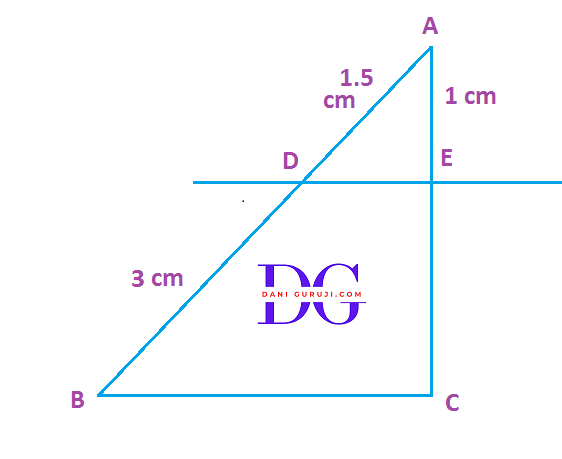
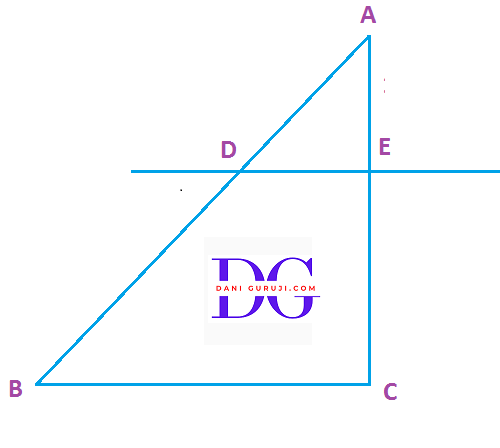
In the following fig. (i)
(i)DE || BC.Find EC in (i)

Solution :

It is given that DE || BC

As per the Basic Proportionality Theorem (B.P.T) or Thales Theorem , we get

( If a line is drawn parallel to one side of a triangle to intersect the other two side in distinct points, the other two sides are divided in the same ratio )

$$ {AD \over BD} = {AE \over EC} $$

Putting the Values

$$⇒ {1.5 \over 3} = {1\over EC} $$

$$⇒ {1.5 × EC} = {3 × 1} $$

$$⇒ { EC} = {3 \over 1.5} $$

$$⇒ { EC} = {2} Cm. $$

Hence, EC = 2 cm.

Question 1 (ii)

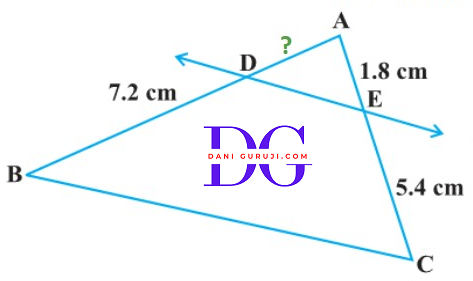
In the following fig. (ii)
(ii) In ∆ABC, DE || BC, AD =?)

Solution :

It is given that DE || BC

As per the Basic Proportionality Theorem (B.P.T) or Thales Theorem , we get

( If a line is drawn parallel to one side of a triangle to intersect the other two side in distinct points, the other two sides are divided in the same ratio )

$$ {AD \over BD} = {AE \over EC} $$

Putting the Values

$$⇒ {AD \over 7.2} = {1.8\over 5.4} $$

$$⇒ {5.4 × AD} = {1.8 × 7.2} $$

$$⇒ { AD} = {{1.8 × 7.2} \over 5.4} $$

$$⇒ { AD} = {{18 × 72 × 10 } \over {54 × 100}} $$

$$⇒ { AD} = {2.4} Cm. $$

Hence, AD = 2.4 cm.

Question 2 (i)

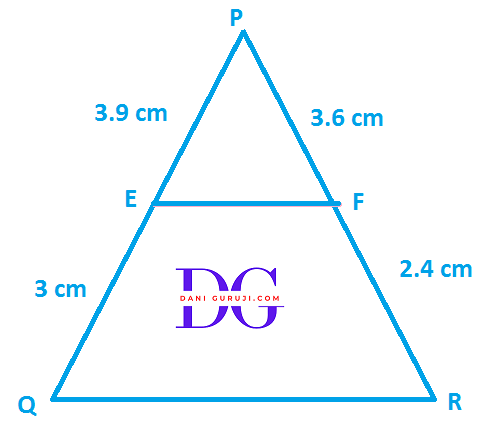
E and F are points on the sides PQ and PR respectively of a PQR For each of the following cases, state whether EF || QR:
(i) PE = 3.9cm. EQ = 3 cm,
PF=3.6cm. FR = 2.4 cm.

Solution :

It is given that

PE = 3.9cm., EQ = 3 cm, PF=3.6cm, FR = 2.4 cm.

As per the Converse of Basic Proportionality Theorem , we get

( We know that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side )

In order to prove EF || QR

We have to prove that

$$ {PE \over EQ} = {PF \over FR} $$

Here,

$${PE \over EQ} = {3.9 \over 3} = 1.3$$

$${PF \over FR} = {3.6 \over 2.4}= {1.5} $$

Hence, $$ {PE \over EQ} {\ne} {PF \over FR} $$

Therefore, EF is not parallel to QR.

Question 2 (ii)

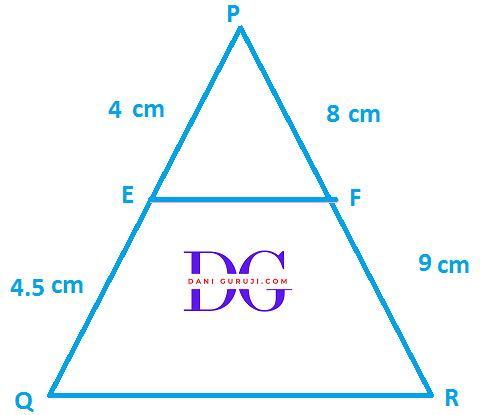
E and F are points on the sides PQ and PR respectively of a PQR For each of the following cases, state whether EF || QR:
(ii) PE = 4 cm. QE = 4.5 cm.
PF = 8 cm. RF = 9 cm.

Solution :

It is given that

PE = 4 cm, QE = 4.5 cm, PF = 8 cm, RF = 9 cm.

As per the Converse of Basic Proportionality Theorem , we get

( We know that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side )

In order to prove EF || QR

We have to prove that

$$ {PE \over EQ} = {PF \over FR} $$

Here,

$${PE \over EQ} = {4 \over 4.5} = = {8 \over 9}$$

$${PF \over FR} = {8 \over 9} $$

Hence, $$ {PE \over EQ} = {PF \over FR} $$

According to converse of Basic Proportionality theorem, EF || QR Therefore, EF is parallel to QR.

Question 2 (iii)

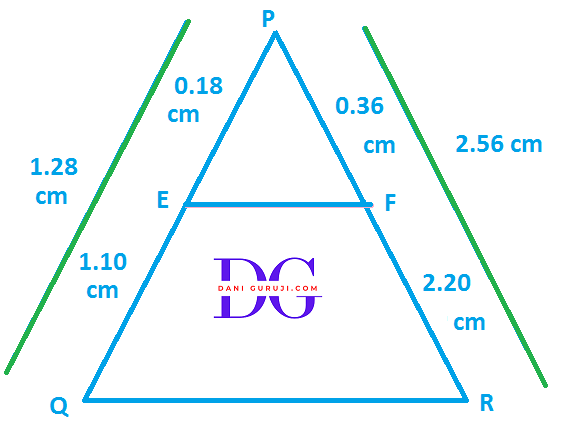
E and F are points on the sides PQ and PR respectively of a PQR For each of the following cases, state whether EF || QR:
(iii) PQ = 1.28 cm. PR = 2.56 cm
PE = 0.18 cm. PF = 0.36 cm.

Solution :

It is given that

PQ = 1.28 cm. PE = 0.18 cm.

PE + EQ = PQ

⇒ EQ = PQ - PE

⇒ EQ = 1.28 - 0.18

⇒ EQ = 1.10 cm

Similarly

PF + FR = PR

⇒ FR = PR - PF

⇒ FR = 2.56 - 0.36

⇒ FR = 2.20 cm

As per the Converse of Basic Proportionality Theorem , we get

( We know that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side )

In order to prove EF || QR

We have to prove that

$$ {PE \over EQ} = {PF \over FR} $$

Here,

$${PE \over EQ} = {0.18 \over 1.10} = {1.8 \over 11}$$

$$⇒ {PE \over EQ} = {18 \over 110} = {9 \over 55}$$

and,

$${PF \over FR} = {0.36 \over 2.20} = {3.6 \over 22} $$

$$⇒ {PF \over FR} = {36 \over 220} = {9 \over 55} $$

Hence, $$ {PE \over EQ} = {PF \over FR} $$

According to converse of Basic Proportionality theorem, EF || QR Therefore, EF is parallel to QR.

Question 3

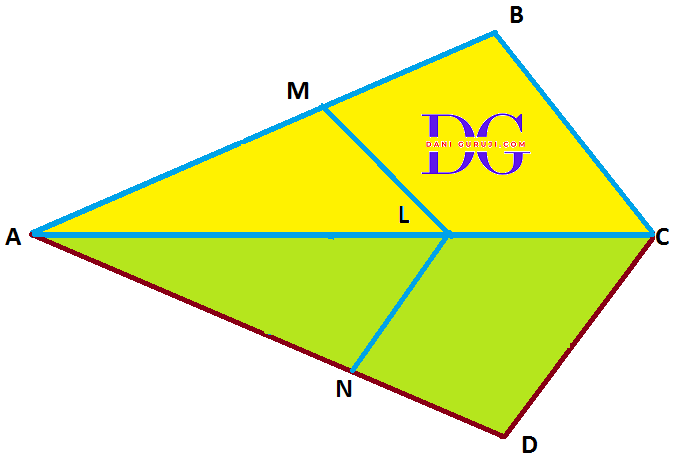
In the following figure. If LM || CB and LN || CD, prove that
$ {AM \over AB} = {AN \over AD} $

Solution :

It is given that

In ∆ACB, LM || CB

As per the Basic Proportionality Theorem (B.P.T), we get

( If a line is drawn parallel to one side of a triangle to intersect the other two side in distinct points, the other two sides are divided in the same ratio )

$$⇒ {AL \over LC} = {AM \over MB} ........ (1) $$

Similarly

In ∆ACD, LN || CD

Therefore by Basic Proportionality Theorem

$$⇒ {AL \over LC} = {AN \over ND} ........ (2) $$

From equation 1 and 2, we get

$$ {AM \over MB} = {AN \over ND} $$

$$⇒ {MB \over AM} = {ND \over AN} $$

Adding 1 on both sides

$$⇒ {MB \over AM} + 1 = {ND \over AN} + 1 $$

$$⇒ {{MB + AM } \over AM} = {{ND + AN }\over AN} $$

$$⇒ {AB \over AM} = {AD \over AN} $$

$$⇒ {AM \over AB} = {AN \over AD} $$

Hence proved $ {AM \over AB} = {AN \over AD} $

Question 4

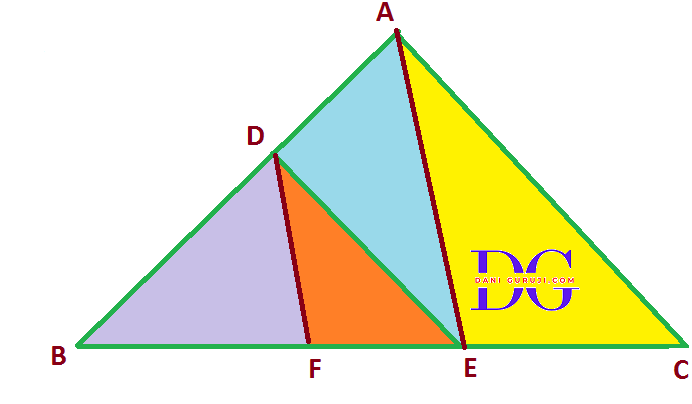
In the following figure , DE ||AC and DF || AE. Prove that
$ {BF \over FE} = {BE \over EC} $

Solution :

It is given that

In ∆ABC, DE ||AC

As per the Basic Proportionality Theorem (B.P.T), we get

( If a line is drawn parallel to one side of a triangle to intersect the other two side in distinct points, the other two sides are divided in the same ratio )

$$⇒ {BD \over AD} = {BE \over EC} ........ (1) $$

Similarly

In ∆AEB, DF || AE

Therefore by Basic Proportionality Theorem

$$⇒ {BF \over FE} = {BD \over AD} ........ (2) $$

From equation 1 and 2, we get

$$ {BF \over FE} = {BE \over EC} $$

Hence proved $ {BF \over FE} = {BE \over EC} $

Question 5

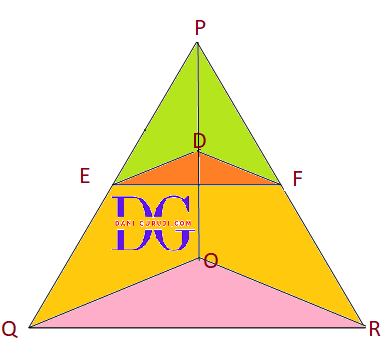
In the following figure, DE || OQ and DF || OR. Show that EF || QR.

Solution :

It is given that

In ∆POQ, DE || OQ

As per the Basic Proportionality Theorem (B.P.T), we get

( If a line is drawn parallel to one side of a triangle to intersect the other two side in distinct points, the other two sides are divided in the same ratio )

$$⇒ {PE \over EQ} = {PD \over DO} ........ (1) $$

Similarly

In ∆PRO, DF || OR

Therefore by Basic Proportionality Theorem

$$⇒ {PF \over FR} = {PD \over DO} ........ (2) $$

From equation 1 and 2, we get

$$ {PE \over EQ} = {PF \over FR} $$

In ∆PQR,

$$ {PE \over EQ} = {PF \over FR} $$

Using converse of Basic Proportionality Theorem

Line EF divides the ∆PQR in the same ratio

$$ ⇒ EF || QR $$

Hence proved

Question 6

In the following figure, A, B and C are points on OP. OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Solution :

It is given that

In ∆POQ, AB || PQ

As per the Basic Proportionality Theorem (B.P.T), we get

( If a line is drawn parallel to one side of a triangle to intersect the other two side in distinct points, the other two sides are divided in the same ratio )

$$⇒ {OA \over AP} = {OB \over BQ} ........ (1) $$

Similarly

In ∆PRO, AC || PR

Therefore by Basic Proportionality Theorem

$$⇒ {OA \over AP} = {OC \over CR} ........ (2) $$

From equation 1 and 2, we get

$$ {OB \over BQ} = {OC \over CR} $$

In ∆OQR,

$$ {OB \over BQ} = {OC \over CR} $$

Using converse of Basic Proportionality Theorem

Line BC divides the ∆OQR in the same ratio

$$ ⇒ BC || QR $$

Hence proved

Question 7

Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).

Solution :

It is given that

In ∆ABC. D is the mid-point of AB.

Let DE is a line passing through the midpoint of line AB and parallel to line BC intersecting line AC at point E.

To Prove: DE bisects AC side at E.

In ∆ABC. D is the mid-point of AB.

Therefore $$ {AD = BD } $$

$$ {AD \over BD} = 1 $$

Now , In ∆ABC DE || BC

As per the Basic Proportionality Theorem (B.P.T), we get

( If a line is drawn parallel to one side of a triangle to intersect the other two side in distinct points, the other two sides are divided in the same ratio )

$$ {AD \over BD} = {AE \over EC} $$

$$ 1 = {AE \over EC} $$

$$ EC = AE $$

⇒ E is Mid Point of AC

Hence proved

Question 8

Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).

Solution :

It is given that

In ∆ABC. D is the mid-point of AB.

To Prove: DE || BC.

In ∆ABC. D is the mid-point of AB.

Therefore, $$ {AD = BD } $$

$$ {AD \over BD} = 1 .....(i)$$

Similarly , In ∆ABC. E is the mid-point of AC.

Therefore, $$ {AE = EC} $$

$$ {AE \over EC} = 1 ....(ii)$$

From (i) and (ii)

$$ {AD \over BD} = {AE \over EC} = 1 $$

$$ {AD \over BD} = {AE \over EC} $$

As per converse of the Basic Proportionality Theorem (B.P.T) or converse of Thales Theorem , we get

( As we know that a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side )

⇒ DE || BC

Hence proved

Question 9

ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that $ {AO \over BO} = {CO \over DO} $ .

Solution :

It is given that

ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O.

To Prove: $ {AO \over BO} = {CO \over DO} $

Construction : EF parallel to AB and CD ( EF||AB , EF||CD ) through point O.

In ∆ABC. .

⇒ $ FO||AB $ ( because Construction EF||AB)

As per the Basic Proportionality Theorem (B.P.T), we get

( If a line is drawn parallel to one side of a triangle to intersect the other two side in distinct points, the other two sides are divided in the same ratio )

$$⇒ {AO \over CO} = {BF \over CF} ..... (i) $$

Similarly , In ∆BCD

⇒ $ FO||CD $ ( because Construction EF||CD)

Therefore by Basic Proportionality Theorem

$$⇒ {BF \over CF} = {BO \over DO} ......(ii)$$

From (i) and (ii)

$$ {AO \over CO} = {BO \over DO} $$

$$ {AO \over BO} = {CO \over DO} $$

Hence proved

Question 10

The diagonals of a quadrilateral ABCD intersect each other at the point O such that $ {AO \over BO} = {CO \over DO} $. Show that ABCD is a trapezium.

Solution :

It is given that

ABCD is a quadrilateral and its diagonals intersect each other at the point O.

$$ {AO \over BO} = {CO \over DO} $$

$$⇒ {AO \over CO} = {BO \over DO} ..... (i) $$

To Prove: ABCD is a trapezium

Construction : EF parallel to AB ( EF||AB ) through point O.

Now , In ∆ABC

⇒ $ FO||AB $ ( because Construction EF||AB)

Therefore by Basic Proportionality Theorem

$$⇒ {AO \over CO} = {BF \over CF} $$

From eq.(i)

$$⇒ {BO \over DO} = {BF \over CF} $$

Thus , In ∆BCD

The line segment FO divides the sides BD and BC in the same proportion

As per converse of the Basic Proportionality Theorem (B.P.T) or converse of Thales Theorem , we get

( As we know that a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side )

$$ FO||DC $$

But we know that FO||AB

Since we initially constructed $ FO||AB $, and we have now shown that $ FO||DC,$ it follows that $ AB||DC$

Therefore, Since one pair of opposite sides is parallel, the quadrilateral ABCD is a trapezium.